Apa Itu Integer (Bilangan Bulat) dan Contohnya?
Bilangan bulat (integer, dibaca: IN-tuh-jer) adalah bilangan utuh (bukan bilangan pecahan) yang bisa bernilai positif, negatif, atau nol.
Contoh bilangan bulat: -5, 1, 5, 8, 97, dan 3.043.
Contoh bilangan yang bukan bilangan bulat: -1,43, 1 3/4, 3,14, 0,09, dan 5.643,1.
Himpunan Bilangan Bulat
Himpunan bilangan bulat, yang dilambangkan dengan Z, secara formal didefinisikan sebagai:
Z = {…, -3, -2, -1, 0, 1, 2, 3, …}
Dalam persamaan matematika, bilangan bulat yang tidak diketahui atau tidak ditentukan biasanya dilambangkan dengan huruf kecil miring dari bagian tengah akhir alfabet. Contoh yang paling umum adalah p, q, r, dan s.
Keunikan Bilangan Bulat
Himpunan Z merupakan himpunan terhitung (denumerable). Ini berarti bahwa meskipun himpunan ini memiliki jumlah elemen yang tak terbatas, semua elemennya tetap dapat dicantumkan dalam daftar yang jelas. Misalnya, dari daftar {…, -3, -2, -1, 0, 1, 2, 3, …}, kita bisa langsung memahami bahwa 356.804.251 dan -67.332 adalah bilangan bulat, tetapi 356.804.251,5, -67.332,89, -4/3, dan 0,232323… bukan.
Hubungan dengan Bilangan Lain
Bilangan bulat dapat dipasangkan satu-satu dengan elemen dalam N, yaitu himpunan bilangan asli. Misalnya, jika N = {1, 2, 3, …}, maka pasangan bisa dibuat seperti ini:
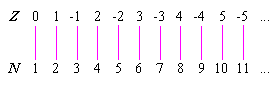
Dalam himpunan tak hingga, keberadaan korespondensi satu-satu seperti ini menjadi acuan dalam menentukan kardinalitas atau ukuran himpunan. Himpunan bilangan asli dan rasional memiliki kardinalitas yang sama dengan Z. Namun, himpunan bilangan real, bilangan imajiner, dan bilangan kompleks memiliki kardinalitas yang lebih besar daripada Z.